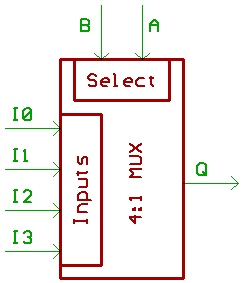
Multiplexers.

Mainly used for routing two, four, or eight data_inputs to one output,
according to the binary value of the Bits at the select lines.

B,A=00 // Q=I0 
B,A=01 // Q=I1 
B,A=10 // Q=I2 
B,A=11 // Q=I3 

Cute, innocent looking little boxes.
But they aren't.

Set the data_inputs to fixed logic levels (constants),
use the select Bits as address lines, and what we finally get
is a small ROM.

Remember, when we used lookup tables in EPROMs
to evaluate logic gates ?
Now an example for abusing the 74151, 8:1 Multiplexer.

Configurated with this lookup table,
the Multiplexer will behave exactly as the gates mentioned above,
but with a smaller propagation delay.
In other words: faster.

Want to put another Inverter into the C line ?
Just swap Bit 0..3 with Bit 4..7 in the lookup table.

If we have a (combinatoral) schematic with logic gates,
three inputs and one output, one 74151 can replace it.

And that's why some FPGAs seem to contain plenty of
multiplexers, that are basically used in the same way.

Now we take a 4:1 Multiplexer, and "turn" the box
counterclockwise by 90 degrees.

The trick is to use the select_inputs as data,
and the data_inputs as select.

What comes out is a configurable logic gate.
According to the Bit pattern at the four select_inputs I0..3,
we can perform any logic operation between the data_inputs
A and B.

0000 = 0x0 // Q=0x00  
1111 = 0xf // Q=0xff  

1010 = 0xa // Q=A     
1100 = 0xc // Q=B     

0101 = 0x5 // Q=/A    
0011 = 0x3 // Q=/B    

1110 = 0xe // Q= A| B 
1101 = 0xd // Q=/A| B 
1011 = 0xb // Q= A|/B 
0111 = 0x7 // Q=/A|/B 

1000 = 0x8 // Q= A& B 
0100 = 0x4 // Q=/A& B 
0010 = 0x2 // Q= A&/B 
0001 = 0x1 // Q=/A&/B 

0110 = 0x6 // Q=  A^B 
1001 = 0x9 // Q=/(A^B)

And if we use eight 4:1 Multiplexers in parallel,
with data_inputs A7..0, B7..0, Outputs Q7..0,
and the select_inputs I3..0 tied together
to all multiplexers, it works as a Logic Unit.

The Arithmetic Part will be attached later.

[HOME] [UP]/ [BACK] [1] [2] [3] [4] [5] [6] [7] [8] [NEXT]

(c) Dieter Mueller 2004